Oceananigans.jl Example: 2D Navier-Stokes Boussinesq Approximation at the Ice-Ocean Interface

This Oceananigans.jl example simulates the melting of sea ice in a two-dimensional setup.

The governing equations are:

\[\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} = -\frac{1}{\rho_0} \nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{g} \rho+\mathbf{F}(z) \\ \nabla \cdot \mathbf{u} = 0\\ \frac{\partial T}{\partial t} + (\mathbf{u} \cdot \nabla) T = \kappa_T \nabla^2 T\\ \frac{\partial S}{\partial t} + (\mathbf{u} \cdot \nabla) S = \kappa_S \nabla^2 S\]

Here, $\mathbf{u} = \mathbf{u}(x,y,z)$ denotes the fluid velocity in m/s, $\rho_0$ is the reference density in $\text{kg/m}^3$, $p$ is the pressure in $\text{dbar}$, $\nu$ is the kinematic viscosity in $\text{m}^2/\text{s}$, $\kappa_S$ is the molecular diffusivity of the salt and $\kappa_T$ is the molecular diffusivity of the temperature in $\text{m}^2/\text{s}$. The term $\mathbf{g}$ represents the gravitational acceleration in $\text{m/s}^2$, and $\rho$ is the fluid density given by:

\[\rho = \rho_0 \left[ 1 - \beta_T (T - T_0) + \beta_S (S - S_0) \right]\]

In this expression:

• $\beta_T$ is the thermal expansion coefficient in $\text{1/K}$,
• $\beta_S$ is the haline contraction coefficient in $\text{1/(g/kg)}$,
• $T$ is the temperature in $\text{K}$,
• $T_0$ is the reference temperature in $\text{K}$,
• $S$ is the salinity in $\text{g/kg}$,
• $S_0$ is the reference salinity in $\text{g/kg}$,

The boundary conditions that simulate the ice-ocean interface are:

• Bottom

\[T=T_\infty = 273 \, \text{K}\\ S=S_\infty = 35 \, \text{g/kg}\]

• Top

\[T_f = 273 + \lambda_1 S + \lambda_2 + \lambda_3 Pb\\ \partial_z S = \left(\frac{\kappa_T}{\kappa_S}\right) \left(\frac{C_p}{L_f}\right) S \partial_z T\]

$T_f$ represents the freezing temperature of water, which decreases as salinity increases, a phenomenon known as salt-induced freezing point depression. This effect occurs because dissolved salts interfere with the formation of ice crystals, requiring a lower temperature for the water to solidify.

Here: \(\lambda_1 = -5.73 \times 10^{-2} \quad \text{K}/(\text{g/kg})\\ \lambda_2 = 8.32 \times 10^{-2} \quad \text{K}\\ \lambda_3 = -7.53 \times 10^{-4} \quad \text{K/dbar}\\ Le = \left( \frac{\kappa_T}{\kappa_s} \right) = [1, 100]\\ C_p = 3974 \quad \text{J}/(\text{K} \text{kg})\\ L_f = 3.35 \times 10^5 \quad \text{J}/\text{kg}\\\)

The salinity and temperature follow the initial conditions as: $T_i(z)=273+(-1-2*z)$ and $S_i(z)=35$.

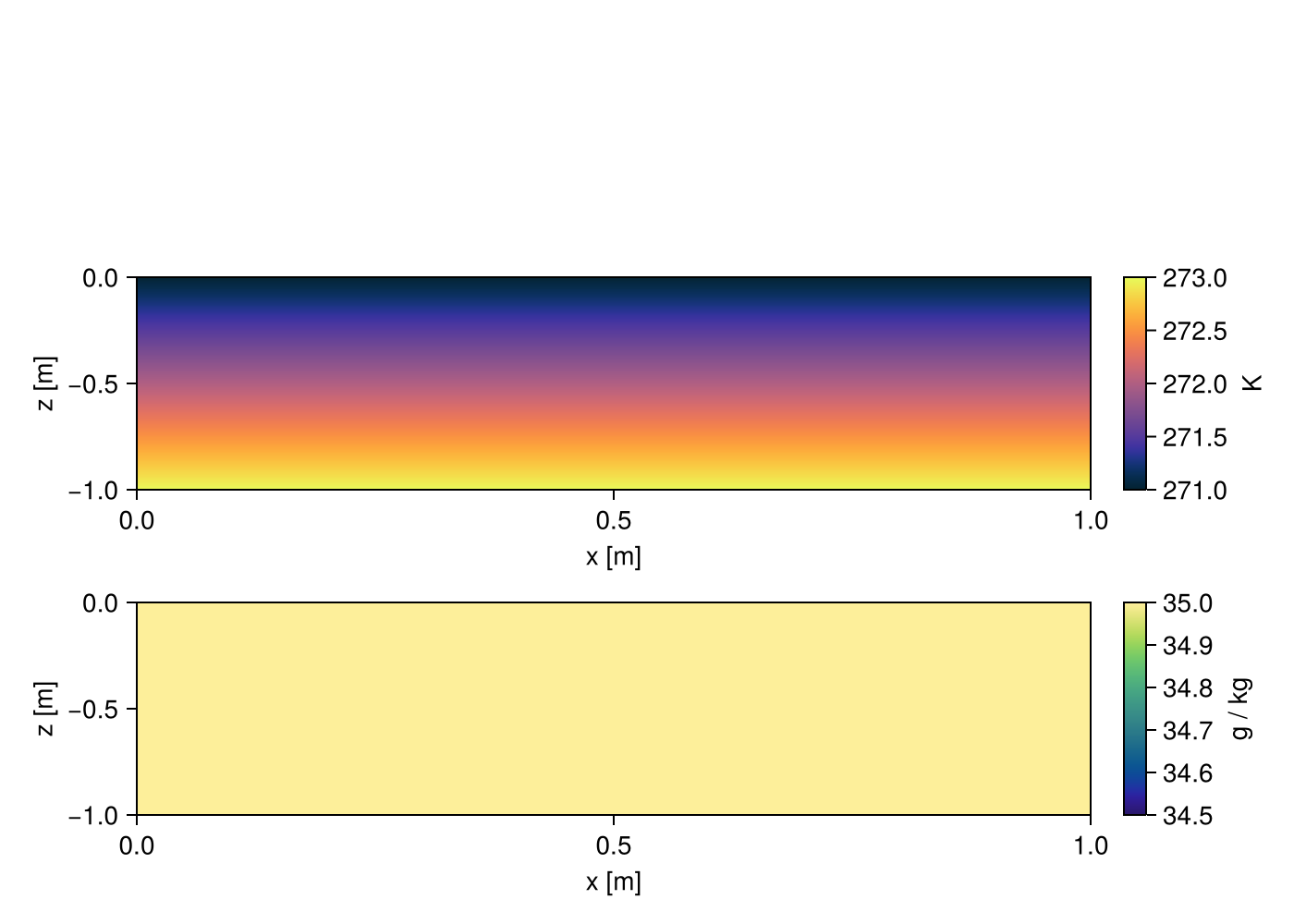
For this example, we set $\text{Le} = 10$, with values of $\kappa_S \approx 10^{-8} , \text{m}^2/\text{s}$ and $\kappa_T \approx 10^{-7} , \text{m}^2/\text{s}$. The video below illustrates the evolution of both tracers. At the ice-ocean boundary, as the ice melts, salinity decreases near the surface, while the temperature of the surrounding water drops. This happens because the melting process absorbs heat from the water, lowering its temperature—a phenomenon known as latent heat absorption, where the heat is used to convert solid ice into liquid water.

To access the Oceananigans.jl file, please download here!